The final result for the total entropy change is
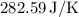
How to calculate the increase in its entropy?
The calculation of the increase in its entropy involves determining the change in entropy and then reconciling the result with the known entropy of graphite at 298K.
Given the equations:
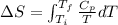
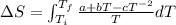
![\(\Delta S = a \ln \left[(T_f)/(T_i)\right] + b (T_f - T_i) + (c)/(2) \left[(1)/(T_f^(2)) - (1)/(T_i^(2))\right]\)](https://img.qammunity.org/2024/formulas/physics/high-school/a6mq26pl50wr0p6oiaqn2ggxiul824xo4b.png)
And applying specific values:
![\(\Delta S = (16.86) \ln \left[(500)/(298)\right] + (4.77 * 10^(-3)) (500 - 298) + ((8.54 * 10^(5)))/(2) \left[(1)/((500)^(2)) - (1)/((298)^(2))\right]\)](https://img.qammunity.org/2024/formulas/physics/high-school/1x1k9nva6s5zggsqrzh3wwow7fjq79dab5.png)
Solving the above expression gives:
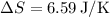
Given that the entropy of graphite at 298K is
 , the total entropy change should be:
, the total entropy change should be:
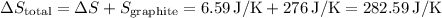
Hence, the final result for the total entropy change is
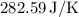 .
.
See image below for complete question.