According to the situation, the domain of this function will contain all values that x can take. Since x is the number of items, it only can take values from 0 to a certain value.
To find this certain value, use the maximum cost allowed (2700) as C(x) and find x using the equation:
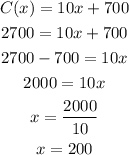
It means that the domain of the function is [0,200]
The range contains all the values that cost can take. We know that the fixed cost (which is the minimum cost) is 700 and the maximum cost is 2700.
It means that the range of the function is [700,2700]