Question

In a sequence, t6 = 50 and tn = 2tn-1 + 5n^2 + n, find the first five terms of the sequence​

Answer 1

To find the first five terms of the sequence, we will plug in the value of t6 in the formula and solve for t5 and further for rest of the required terms.

t5

t6 = 2t6 - 1 + 5(6^2) + 6

t6 = 2t5 + 5 x 36 + 6

t6 = 2t5 + 180 + 6

t6 = 2t5 + 186

2t5 + 186 = 50

2t5 = 50 - 186

t5 = -136/2

t5 = -68

t4

t5 = 2t5 - 1 +5(5^2) + 5

t5 = 2t4 + 5 x 25 + 5

t5 = 2t4 + 125 + 5

t5 = 2t4 + 130

2t4 + 130 = -68

2t4 = -68 -130

t4 = -198/2

t4 = -99

t3

t4 =2t4 - 1 + 5(4^2) + 4

t4 = 2t3 + 5 x 16 + 4

t4 = 2t3 + 80 + 4

t4 = 2t3 + 84

2t3 +84 = -99

2t3 = -99 -84

t3 =-183/2

t3 = -91.5

t2

t3 = 2t3 - 1 + 5(3^2) + 3

t3 = 2t2 + 5 x 9 + 3

t3 = 2t2 + 45 + 3

t3 = 2t2 + 48

2t2 + 48 = -91.5

2t2 = -91.5 - 48

t2 = -139.5/2

t2 = -69.75

t1

t2 = 2t2 - 1 + 5(2^2) + 2

t2 = 2t1 + 5 x 4 + 2

t2 = 2t1 + 20 + 2

t2 = 2t1 + 22

2t1 + 22 = -69.75

2t1 = -69.75 -22

t1 = -91.75/2

t1 = -45.875

Thus, our first five terms of the sequence are -45.875, -69.75,-91.5,-99 and -68.

Answer 2

t₁ = -45.875

t₂ = -69.75

t₃ = -91.5

t₄ = -99

t₅ = -68

Explanation:

Given recursive sequence:

`\begin{cases}t_6=50\\t_n=2t_(n-1)+5n^2+n\end{cases}`

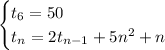
A recursive rule for a sequence is a formula that generates each term in the sequence based on the previous term.

To find the first five terms of the sequence, we can use the recursive formula to calculate each term one by one.

We have been given the sixth term of the sequence, t₆ = 50.

To find the fifth term (t₅) substitute n = 6 into the formula, set it to 50, then solve for t₅:

`\begin{aligned}t_6&=50\\2t_(6-1)+5(6)^2+(6)&=50\\2t_(5)+5(36)+6&=50\\2t_(5)+180+6&=50\\2t_(5)+186&=50\\2t_(5)&=-136\\t_(5)&=-68\end{aligned}`

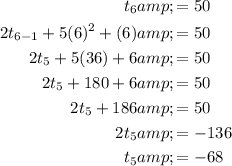
To find the fourth term, t₄, substitute n = 5 into the formula, set it to -68, then solve for t₄:

`\begin{aligned}t_5&=-68\\2t_(5-1)+5(5)^2+(5)&=-68\\2t_(4)+5(25)+5&=-68\\2t_(4)+125+5&=-68\\2t_(4)+130&=-68\\2t_(4)&=-198\\t_(4)&=-99\end{aligned}`

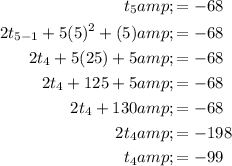
To find the third term, t₃, substitute n = 4 into the formula, set it to -99, then solve for t₃:

`\begin{aligned}t_4&=-99\\2t_(4-1)+5(4)^2+(4)&=-99\\2t_(3)+5(16)+4&=-99\\2t_(3)+80+4&=-99\\2t_(3)+84&=-99\\2t_(3)&=-183\\t_(3)&=-91.5\end{aligned}`

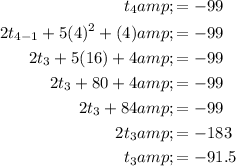
To find the second term, t₂, substitute n = 3 into the formula, set it to -91.5, then solve for t₂:

`\begin{aligned}t_3&=-91.5\\2t_(3-1)+5(3)^2+(3)&=-91.5\\2t_(2)+5(9)+3&=-91.5\\2t_(2)+45+3&=-91.5\\2t_(2)+48&=-91.5\\2t_(2)&=-139.5\\t_(2)&=-69.75\end{aligned}`

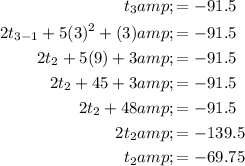
To find the first term, t₁, substitute n = 2 into the formula, set it to -69.75, then solve for t₁:

`\begin{aligned}t_2&=-69.75\\2t_(2-1)+5(2)^2+(2)&=-69.75\\2t_(1)+5(4)+2&=-69.75\\2t_(1)+20+2&=-69.75\\2t_(1)+22&=-69.75\\2t_(1)&=-91.75\\t_(1)&=-45.875\end{aligned}`

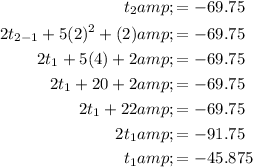
So, the first five terms of the sequence are:

• t₁ = -45.875
• t₂ = -69.75
• t₃ = -91.5
• t₄ = -99
• t₅ = -68