Question

What should be multiplied to x^2 - 6x +23 to get product x^3 - 2x^2 - x + 92​

Answer 1

x - 4

Explanation:

To find the polynomial that, when multiplied by x² - 6x + 23, results in x³ - 2x² - x + 92, we can use polynomial long division.

Divide x³ - 2x² - x + 92 by x² - 6x + 23:

`\large \begin{array}{r}x+4\phantom{)..}\\x^2 - 6x +23{\overline{\smash{\big)}\,x^3 - 2x^2- \phantom{.))} x + 92\phantom{)}}\\{-~\phantom{(}\underline{(x^3-6x^2+23x)\phantom{...))))}}\\4x^2-24x\phantom{....))))}\\-~\phantom{()}\underline{(4x^2-24x+92)}\\0\phantom{)}\\\end{array}`

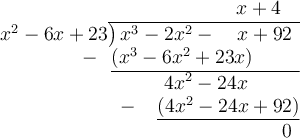
So, the polynomial that should be multiplied to x² - 6x + 23 to get the product x³ - 2x² - x + 92 is:

`\Large\boxed{\boxed{x + 4}}`

`\hrulefill`

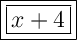
Check by multiplying x + 4 by x² - 6x + 23:

`\begin{aligned}(x+4)(x^2-6x+23)&=x(x^2-6x+23)+4(x^2-6x+23)\\\\&=x^3-6x^2+23x+4x^2-24x+92\\\\&=x^3-2x^2-x+92 \end{aligned}`

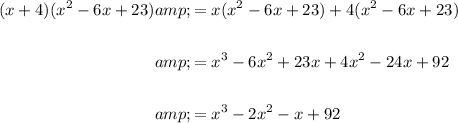
This confirms that the product of x + 4 and x² - 6x + 23 is x³ - 2x² - x + 92.