Question

The position of a baseball (in ft) is represented by r(t) = 55 2 ti + (3 + 55 2 t − 16t2)j. Find the arc length of the trajectory (flight) of the baseball. (Let t = 0 represent when the ball is hit.

Answer 1

To find the arc length of the trajectory of the baseball, we need to calculate the magnitude of the velocity vector and integrate it over the time interval represented by the roots of the quadratic equation. Thus, the arc length of the trajectory is approximately 296.45 feet.

Step-by-step explanation:

To find the arc length of the trajectory of the baseball, we need to integrate the magnitude of the velocity vector with respect to time.

The velocity vector is given by the derivative of the position vector, so we first need to find the derivative of the given position function:

r'(t) = {55√2}i + (55 √2 - 32t)j

Now, we can calculate the magnitude of the velocity vector:

|v(t)| = √{(55 √{2})² + (55 √{2} - 32t)²}

Next, we integrate this magnitude over the time interval represented by the roots of the quadratic equation to find the arc length:

S =
`\int_(0.54)^(3.79) \sqrt{(55 √(2))^2 + (55 √(2) - 32t)^2} dt`

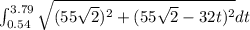
Solving this integral will give us the arc length of the trajectory of the baseball.

To solve this integral, first, simplify the expression under the square root:

S =
`\int_(0.54)^(3.79) \sqrt{(6050 + (55 √(2) - 32t)^2} dt`

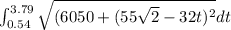
Now, integrate with respect to t:

S =
`\int_(0.54)^(3.79) √((6050 + (55^2 . 2 - 2 . 55 . 32t + 32t)^2) dt`

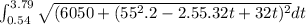
Now, let's factor the quadratic under the square root:

S =
`\int_(0.54)^(3.79) √(( 32t + 161t)^2) dt`

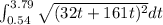
S =
`\int_(0.54)^(3.79) \s32t + 161t dt`

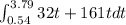
Now, integrate:

S = (16 x 3.79² - 161 x 3.79) - (16 x 0.54² - 161 x 0.54)

S = -296.4496

So, the arc length of the trajectory is approximately 296.45 feet.

Note that the negative sign in the result indicates that the path is traversed in the opposite direction (decreasing t).

In the context of arc length, we are usually interested in the magnitude, so you can take the absolute value, and the arc length is approximately 296.45 feet.