Question

Can you explain.Use the intermediate value theorem for polynomials to show that the polynomial function has a real zero between the numbers given.f(x) = -6x^4+5x^2+4;-2 and -1

Answer 1

We are to show that the given polynomial function has a real zero between the numbers given.

`f(x)=-6x^4+5x^2\text{ + 4}`

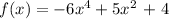
At x = -2, we substitute -2 for x in the given function;

`\begin{gathered} f(-2)=-6(-2)^4+5(-2)^2\text{ + 4} \\ f(-2)\text{ = -6(16) + 5(4) + 4} \\ f(-2_{})\text{ = -96 + 20 + 4} \\ f(-2)\text{ = -72} \end{gathered}`

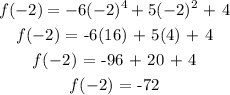
At x = -1, we substitute -1 for x in the given function;

`\begin{gathered} f(-1)=-6(-1)^4+5(-1)^2\text{ + 4} \\ f(-1)\text{ = -6(1) + 5(1) + 4} \\ f(-1)\text{ = -6 + 5 + 4} \\ f(-1)\text{ = 3} \end{gathered}`

CONCLUSION:

Since the function f went from -72 to +3 over the interval of -2 to -1, that means it must have passed through zero.