SOLUTION:
We are to show that the given polynomial function has a real zero between the numbers given.

At x = -2, we substitute -2 for x in the given function;
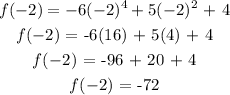
At x = -1, we substitute -1 for x in the given function;
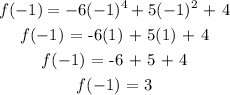
CONCLUSION:
Since the function f went from -72 to +3 over the interval of -2 to -1, that means it must have passed through zero.