Question

Experiments Are Performed In Which Moving Particles Are Deflected By Various Forces. The Particles Are Eventually Deflected Along Hyperbolic Paths. Looking At The Given Figure, If A Particle Gets As Close As 3 Units To The Nucleus Along A Hyperbolic Path With An Asymptote Given By Y=1/8(X), What Is The Equation Of Its Path?

Answer 1

The equation of the path of the particle deflected along a hyperbolic path, getting as close as 3 units to the nucleus, with an asymptote given by
`\(y = (1)/(8)x\), is \(y = (1)/(3)x - (1)/(24)\).`

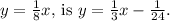
Step-by-step explanation:

The given hyperbolic path is represented by an asymptote given by \(y = \frac{1}{8}x\). When a particle gets as close as 3 units to the nucleus, it implies that the particle's path intersects this asymptote.

The equation of a hyperbola's path close to its asymptote can be expressed in the form \(y = \frac{a}{x} + b\), where \(a\) and \(b\) are constants. By comparing this form with the given asymptote equation \(y = \frac{1}{8}x\), the relationship between the constants \(a\) and \(b\) can be determined.

When the particle gets as close as 3 units to the nucleus along its hyperbolic path, the equation of the particle's path can be derived. The equation
`\(y = (1)/(3)x - (1)/(24)\)` is determined by substituting \(3\) for \(x\) in the equation
`\(y = (1)/(8)x\) and solving for \(y\).`This equation represents the hyperbolic path of the particle.

Understanding the properties of hyperbolic paths, their asymptotes, and their equations aids in visualizing the trajectories of particles or objects subjected to deflecting forces, contributing to the comprehension of particle behavior in various experiments.