Question

The length of a rectangle is 10 cm, and its perimeter is less than 34 cm. What can you conclude about its width?

Answer 1

W < 7

Explanation:

The perimeter (P) of a rectangle can be calculated using the formula:

`\sf P = 2L + 2W`

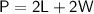
• Where L is the length of the rectangle, and W is the width.
• In this case, the rectangle's length is 10 cm, so L = 10
• The problem states that the perimeter is less than 34 cm.

Therefore, we can write:

`\sf2L + 2W < 34`

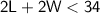
Substitute the value of L

`\sf 2(10) + 2W < 34`

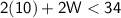
Now, simplify the equation:

`\sf 20 + 2W < 34`

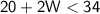
Subtract 20 from both sides:

`\sf 2W < 14`

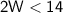
Finally, divide by 2:

`\sf W < 7`

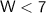
So, the width of the rectangle must be less than 7 cm in order for the perimeter to be less than 34 cm.

Answer 2

The width must be less than 7.

Explanation:

We know that the perimeter of a rectangle is given by

P = 2(l+w)

The perimeter is less than 34

34 > 2 (l+w)

34 > 2 (10+w)

Divide each side by 2

17 > 10+w

Subtract 10 from each side

17-10 > w

7 > w

The width must be less than 7.