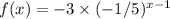The correct option is D) f(x) = -(1)/(5) * (-3)ˣ⁻¹.
The given sequence is: -3, 3/5, -(3)/(25), (3)/(125), -(3)/(625).
Let's express each term in terms of the first term (-3):
First term: -3
Second term: (-3) / (-5) = 3/5
Third term: (3/5) / (-5) = -(3)/(25)
Fourth term: (-(3)/(25)) / (-5) = (3)/(125)
Fifth term: ((3)/(125)) / (-5) = -(3)/(625)
Now, let's generalize the pattern:
The nth term can be obtained by taking the first term (-3) and multiplying it by
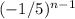
So, the correct formula for the sequence is: