Question

Find the measure of ABD and DBC given ABC = 140°.

Answer 1

<ABD = 72, <DBC=68

Explanation:

To do this you first want to and them together:

(4x-8) + (3x+8) = 4x-8+3x+8 = 7x

You know that <ABC is 140

So 7x = 140, x=20

Then replace x in each of the equations

80-8 , 60+8

So the answer is:

<ABD = 72 and <DBC = 68

Answer 2

m ∠ABD = 72°

m ∠DBC = 68°

Explanation:

Given:

• m ∠ABD = 4x - 8
• m ∠DBC = 3x + 8
• m ∠ABC = 140°

To find:

• m ∠ABD
• m ∠DBC

Solution:

Since m ∠ABC is the sum of m ∠ABD and m ∠DBC.

So, we can setup equation as:

m ∠ABC = ∠ABD + m ∠DBC

Substitute the given value:

140 = 4x - 8 + 3x + 8

Simplify like terms:

140 = 7x

Divide both sides by 7.

`\sf (140 )/(7) =( 7x )/(7)`

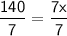
x = 20

Now, we can find the measure of m ∠ABD and m ∠DBC by substituting value of x.

So,

m ∠ABD = 4 × 20 - 8 = 80 - 8 = 72°

m ∠DBC = 3 × 20 + 8 = 60 + 8 = 68°

Therefore, the measure of:

m ∠ABD = 72°

m ∠DBC = 68°