There is no solution to the equation sec2β−1/tan(−β) =1 at intervals −π ≤ β < π.
Solving trigonometry equations.
To find all the solutions to the equation sec²β - 1/tan(-β) = 1 for which -π ≤ β < π, we need to first solve the trigonometry equation first using the appropriate notations.
Given:
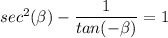
 can be written as
can be written as
 because
because
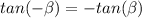

Let write tan β in terms of sin (β) and cos (β)
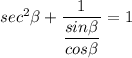
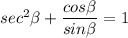
Similarly, sec²β can be written in terms of sinβ and cosβ
i.e.
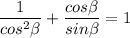
Solving the fractions by using a factor with common denominator, we have:

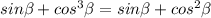
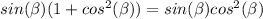
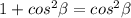
Therefore, we can conclude that there is no solution to the intervals at −π ≤ β < π.