Question

What is the slope of the line whose equation is 12= 4x-6y

Answer 1

Answer: m = -2/3

Explanation:

We are asked to calculate the slope of the following line:

`\longrightarrow\quad\sf{12=4x-6y}`

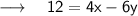
But before we start, let's rearrange our equation. We'll write it in slope intercept form.

So first, we write it this way:

`\longrightarrow\quad\sf{4x-6y=12}`

Next, we subtract 4x from both sides:

`\longrightarrow\quad\sf{-6y=12-4x}`

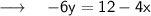
Next, divide both sides by -6:

`\longrightarrow\quad\sf{y=\cfrac{12}{-6}-\cfrac{-4x}{-6}}`

`\longrightarrow\quad\sf{y=-2-\cfrac{4}{6}x}`

`\longrightarrow\quad\sf{y=-\cfrac{2}{3}x-2}`

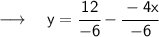
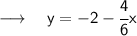
Our equation is now in slope-intercept form. The next step is to find the slope, which is the number in front of x. In this case, this number is -2/3.

Therefore, the slope is -2/3.

Answer 2

The slope of the line is 2/3.

Explanation:

In order to find the slope of the line with the equation
`12 = 4x - 6y`, we need to rearrange the equation into slope-intercept form, which is
`y = mx + b`, where m is the slope.

First, let's isolate y on one side of the equation:

`\large\begin{aligned} 12 &= 4x - 6y \\ 6y &= 4x - 12 \\ y &= (4)/(6)x - (12)/(6) \\ y &= (2)/(3)x - 2 \end{aligned}`

Now we can see that the slope is 2/3.