Question

Please answer carefully

Transfer to standard form and find solution

1. (S+6)² = 36

`2. \: (2)/(t) - (3t)/(2) = 7`
​

Answer 1

1) s = 0 , -12

2) t = (√61-7)/3 and (-√61-7)/3

Explanation:

#Question 1 :-

Given :

• ( s + 6 )² = 36

We have to find ,

• Value of s

Solution :

`\longmapsto \: \: \: \sf{(s + 6) {}^(2) = 36}`

We know that ,

• ( a + b )² = a² + b² + 2ab

`\longmapsto \: \: \: \sf{s{}^(2) + 36 + 2(6)(s) = 36}`

`\longmapsto \: \: \: \sf{s{}^(2) + 36 + 12s = 36}`

Subtracting 36 on both sides :

`\longmapsto \: \: \: \sf{s{}^(2) + \cancel{36 } + 12s - \cancel{36}= 36 - 36}`

We get ,

`\longmapsto \: \: \: \sf{s {}^(2) + 12s = 0 }`

Taking s common :

`\longmapsto \: \: \: \sf{s (s + 12) = 0 }`

Now we can see that product of two things that are s and ( s + 12 ) gives 0 , which means one of them or both can be 0. Therefore , comparing both with 0 :

`\longmapsto \: \: \: \underline{ \boxed{ \sf{ \bold{s = 0 }}}} \: \: \: \bigstar`

and ,

`\longmapsto \: \: \: \sf{s + 12= 0 }`

Subtracting 12 on both sides :

`\longmapsto \: \: \: \sf{s + \cancel{12 }- \cancel{12}= 0 - 12 }`

We get ,

`\longmapsto \: \: \: \underline{ \boxed{ \sf{ \bold{s = = - 12}}}} \: \: \: \bigstar`

• Therefore , value of s is "0" and "-12"

Verification:

#When s = 0 :

• ( s + 6 )² = 36

• ( 0 + 6 )² = 36

• (6)² = 36

• 36 = 36

• LHS = RHS

• Hence , Verified

#When s = -12

• ( s 6 )² = 36

• ( -12 + 6 )² = 36

• ( -6 )² = 36

• 36 = 36

• LHS = RHS

• Hence, Verified

Therefore , our answer is correct! :)

#Question 2 :

Given ,

• 
  `\sf{(2)/(t) -(3t)/(2) =7}`

We have to find ,

• Value of t

Solution :

`\dashrightarrow\:\:\:\sf{(2)/(t) -(3t)/(2) =7}`

Simplifying Left Hand side by Taking Least Common Factor of t and 2 that is 2t :

`\dashrightarrow\:\:\:\sf{(2(2)-t(3t))/(2t) =7}`

We get ,

`\dashrightarrow\:\:\:\sf{((4)-(3t^(2) ))/(2t) =7}`

Multiplying both sides with 2t :

`\dashrightarrow\:\:\:\sf{\frac{(4)-(3t^(2) )}{\cancel{2t}} * \cancel{2t}=7* 2t}`

We get ,

`\dashrightarrow\:\:\:\sf{(4)-(3t^(2) )=14t}`

Subtracting 14t on both sides :

`\dashrightarrow\:\:\:\sf{(4)-(3t^(2) )-14t=\cancel{14t}-\cancel{14t}}`

`\dashrightarrow\:\:\:\sf{-3t^(2) -14t + 4=0}`

Taking negative sign common :

`\dashrightarrow\:\:\:\sf{-(3t^(2) +14t - 4)=0}`

So the quadratic equation formed is :

`\dashrightarrow\:\:\:\sf{3t^(2) +14t - 4=0}`

Now , we are solving the quadratic equation using Quadratic formula. Quadratic Formula is :

`\: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \boxed{\sf{t=\frac{-b\:\pm\:\sqrt{b^(2) -4ac} }{2a} }}`

Where ,

• a = 3

• b = 14

• c = -4

`\implies \: \: \sf{t=\frac{-14\:\pm\sqrt{(14)^(2)-4(3)(-4) } }{2(3)}}`

Simplifying :

`\implies \: \: \sf{t=(-14\:\pm√(196 + 48) )/(6)}`

`\implies \: \: \sf{t=(-14\:\pm√(244 ) )/(6)}`

`\implies \: \: \sf{t=(-14\:\pm2√(61 ) )/(6)}`

Separating negative and positive values :

`\longmapsto \: \: \: \sf{t = ( - 14 + 2 √(61) )/( 6)}`

Taking 2 common from numerator :

`\longmapsto \: \: \: \sf{t = \frac{ \cancel{2}( - 7 + √(61) )}{ \cancel{ 6}}}`

We get ,

`\longmapsto \: \: \: \underline{ \boxed{\sf{ \bold{t= ( √(61)-7 )/( 3)}}}} \: \: \: \bigstar`

Now , other value of t :

`\longmapsto \: \: \: \sf{t = ( - 14 - 2 √(61) )/( 6)}`

Taking -2 common from numerator :

`\longmapsto \: \: \: \sf{t = \frac{ - \cancel{ 2}(7 + √(61)) }{ \cancel{ 6}}}`

We get ,

`\longmapsto \: \: \: \underline{ \boxed{\sf{t = \bold{( -√(61) - 7)/( 3)}}}} \: \: \: \bigstar`

Hope, it'll help you!!

Answer 2

S = either 0 or -12

t = either
`( -7 + √(61))/(3 )` or

`( -7 - √(61))/(3 )`

Explanation:

1st Question:

(S+6)² = 36

Let's solve using factoring root method:

The factoring root method is a method for solving quadratic equations by factoring the quadratic expression and then setting each factor equal to zero and solving for the roots.

In this case:

(S+6)² = 36

Subtract 36 on both sides:

(S+6)² - 36 = 36 - 36

(S+6)² - 36 = 0

Since 36 = 6², we have

(S+6)² - 6² =0

Using formula: a² - b² = (a+b)(a-b), we get

(S+6+6)(S+6-6) = 0

(S+12)(S) = 0

Either

S = 0

Or

S + 12 = 0

S = -12

Therefore, the value of S is either 0 or -12.

2nd Question:

`\sf (2)/(t) - (3t)/(2) = 7`

let's solve it using the quadratic equation formula:

The quadratic formula is a formula that can be used to solve any quadratic equation of the form ax² + bx + c = 0, where a, b and c are real numbers.

The quadratic formula is given by:

`\sf x = (-b \pm √(b^2 - 4ac))/(2a)`

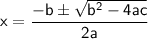
To solve the equation using the quadratic formula, we first need to rewrite it in the form ax² + bx + c = 0. We can do this by multiplying both sides of the equation by 2t:

`\sf 2t \left( (2)/(t) - (3t)/(2) \right) = 2t \cdot 7`

`\sf 4 - 3t^2 = 14t`

`\sf -3t^2 - 14t + 4 = 0`

Multiply both sides by -1, we get

`\sf -1(-3t^2 - 14t + 4 )= 0`

`\sf 3t^2 + 14t - 4 = 0`

Now, we can identify the coefficients a, b and c of the quadratic equation:

• a = 3
• b = 14
• c = -4

Substituting these values into the quadratic formula and evaluate, we get:

`\begin{aligned} t & = (-14 \pm √((14)^2 - 4 \cdot 3 \cdot -4))/(2 \cdot 3) \\\\ & = (-14 \pm √(244))/(6) \\\\ &= (-14 \pm 2√(61))/(6) \end{aligned}`

It has two values,

When positive

`\begin{aligned} t & = (-14 + 2√(61))/(-6) \\\\ & = \frac{\cancel{2}(-7 + √(61)}{\cancel{2}\cdot3} \\\\ & = ( -7 + √(61))/(3 ) \end{aligned}`

When negative

`\begin{aligned} t & = (-14 - 2√(61))/(-6) \\\\ & = \frac{\cancel{2}(-7 - √(61)}{\cancel{2}\cdot3} \\\\ & = ( -7 - √(61))/(3 ) \end{aligned}`

Therefore, the solutions to the equation is:

`t = ( -7 + √(61))/(3 )`

or

`t = ( -7 - √(61))/(3 )`