Question

An ellipse whose center is at the origin and has an endpoint (4,0) and a focus of (0,3).

A) What ellipse form should be used given the above information?Explain why this form was chose.
B) Write an equation for the ellipse and solve for any needed information.
C) Find the length of the major and minor of the ellipse.

Answer 1

Check the picture below.

so the ellipse looks more or less like the one in the picture, hmmm so we know one focus point at (0,3), and an endpoint at (4,0), the endpoint gives us more or less the conjugate axis, assuming we use the origin at its center, that puts the other focus point at (0,-3), as you see in the picture.

A) what form to use?

well, if we use the origin as its center, that means the major axis is vertical, so the "a" component must be in the fraction with the "y" variable, so

`\textit{ellipse, vertical major axis} \\\\ \cfrac{(x- h)^2}{ b^2}+\cfrac{(y- k)^2}{ a^2}=1`

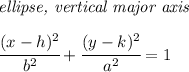
B)

`\textit{ellipse, vertical major axis} \\\\ \cfrac{(x- h)^2}{ b^2}+\cfrac{(y- k)^2}{ a^2}=1 \qquad \begin{cases} center\ ( h, k)\\ vertices\ ( h, k\pm a)\\ c=\textit{distance from}\\ \qquad \textit{center to foci}\\ \qquad √( a ^2- b ^2) \end{cases} \\\\[-0.35em] ~\dotfill`

`\begin{cases} h=0\\ k=0\\ b=4\\ c=3 \end{cases}\implies \cfrac{(x- 0)^2}{ 4^2}+\cfrac{(y- 0)^2}{ a^2}=1 \\\\\\ c=√(a^2-b^2)\implies 3=√(a^2-4^2)\implies 9=a^2-16 \\\\\\ 25=a^2\implies √(25)=a\implies 5=a \\\\[-0.35em] ~\dotfill\\\\ \cfrac{(x- 0)^2}{ 4^2}+\cfrac{(y- 0)^2}{ 5^2}=1\implies \boxed{\cfrac{x^2}{16}+\cfrac{y^2}{25}=1}`

C)

major is simply 5 + 5 = 10

minor is just 4 + 4 = 8.