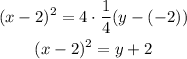Question

The coordinates of the focus are (2,-7/4), the coordinates of the endpoints of the latus rectum are (3/2,-7/4) and (5/2,-7/4). The equation of the directions is y=-9/4, and the equation of the axis of symmetry is x=2.

Answer 1

General equation of a parabola:

`(x-h)^2=4p(y-k)`

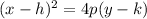
Equation of the axis of symmetry:

x = h

In this case, the axis of symmetry is x = 2, then h = 2.

Equation of the directrix:

y = k - p

In this case, the equation of the directrix is y = -9/4, then:

-9/4 = k - p (eq. 1)

Equation of the focus:

F(h, k+p)

In this case, the coordinates of the focus are (2,-7/4), then:

-7/4 = k + p (eq. 2)

Adding equation 1 to equation 2:

-9/4 = k - p

+

-7/4 = k + p

--------------------

-4 = 2k

(-4)/2 = k

-2 = k

Substituting this result into equation 2 and solving for p:

-7/4 = -2 + p

-7/4 + 2 = p

1/4 = p

Substituting with h = 2, k = -2, and p = 1/4 into the general equation, we get:

`\begin{gathered} (x-2)^2=4\cdot(1)/(4)(y-(-2)) \\ (x-2)^2=y+2 \end{gathered}`