Question

A wave traveling on a Slinky® that is stretched to 4 m takes 4.97 s to travel the length of the Slinky and back again.(a) What is the speed (in m/s) of the wave? 1.61 m/s b) Using the same Slinky® stretched to the same length, a standing wave is created which consists of seven antinodes and eight nodes. At what frequency (in Hz) must the Slinky be oscillating? Hz =

Answer 1

The speed of the wave is 1.61 m/s, and the frequency of the standing wave is 3.22 Hz.

Step-by-step explanation:

(a) To find the speed of the wave, we can use the formula:

Speed = Distance / Time

In this case, the distance traveled by the wave is twice the length of the Slinky, which is 8 meters. The time taken for the wave to travel this distance is 4.97 seconds.

Therefore, the speed of the wave is:

Speed = 8 meters / 4.97 seconds = 1.61 m/s

(b) The frequency of the standing wave can be determined using the formula:

Frequency = (Number of Antinodes + 1) × (Speed / Wavelength)

In this case, the number of antinodes is 7 and the wavelength can be calculated by dividing the length of the Slinky by the number of nodes plus 1 (8 + 1). So the wavelength is 4 meters.

Using these values, the frequency of the standing wave is:

Frequency = (7 + 1) × (1.61 m/s / 4 m) = 3.22 Hz

Answer 2

Given:

The length of the slinky is: L = 4 m.

The time taken by the wave to travel the length and back again is: t = 4.97 s

To find:

a) The speed of the wave

b) The frequency of the wave

Step-by-step explanation:

a)

As the wave on the slinky travels along the length and back again, it covers a distance that is double the distance of the slinky.

Thus, the total distance "d" traveled by the wave will be 2L.

The speed "v" of the wave is given as:

`\begin{gathered} v=(d)/(t) \\ \\ v=(2L)/(t) \end{gathered}`

Substituting the values in the above equation, we get:

`\begin{gathered} v=\frac{2*4\text{ m}}{4.97\text{ s}} \\ \\ v=\frac{8\text{ m}}{4.97\text{ s}} \\ \\ v=1.61\text{ m/s} \end{gathered}`

Thus, the speed of the wave is 1.61 m/s

b)

The standing wave created consists of seven antinodes and eight nodes. Thus, the length of the slinky is 7/2 times the wavelength of the wave.

`L=(7)/(2)\lambda`

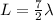
Rearranging the above equation, we get:

`\lambda=(2)/(7)L`

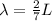
Substituting the values in the above equation, we get:

`\lambda=(2)/(7)*4\text{ m}=\frac{8\text{ m}}{7}=1.143\text{ m}`

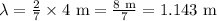
The speed "v" of the wave is related to its wavelength "λ" and a frequency "f" as:

`v=f\lambda`

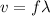
Rearranging the above equation, we get:

`f=(v)/(\lambda)`

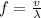
Substituting the values in the above equation, we get:

`\begin{gathered} f=\frac{1.61\text{ m/s}}{1.143\text{ m}} \\ \\ f=1.41\text{ Hz} \end{gathered}`

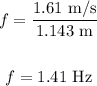
Thus, the frequency of the wave on the slinky is 1.41 Hz.

Final answer:

a) The speed of the wave is 1.61 m/s.

b) The frequency of the oscillation of the slinky is 1.41 Hz.