Final Answer:
C) The average cost of producing 20 lawn mowers.
Step-by-step explanation:
The marginal average cost at
 denoted as
denoted as
 , represents the rate of change of the average cost with respect to the number of lawn mowers produced. Mathematically,
, represents the rate of change of the average cost with respect to the number of lawn mowers produced. Mathematically,
 is the derivative of the total cost function
is the derivative of the total cost function
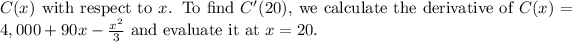
![\[ C'(x) = 90 - (2x)/(3) \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/c83vytstezj6ezapv6rout59wbu416uv36.png)
Substitute

![\[ C'(20) = 90 - (2 * 20)/(3) = 90 - (40)/(3) = (270 - 40)/(3) = (230)/(3) \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/fuluut9e1uh8f03tn7tmdgoyft9l0a2jcx.png)
So,
 is the rate of change of the average cost at
is the rate of change of the average cost at
 This represents how the average cost changes when producing one more lawn mower at that specific production level.
This represents how the average cost changes when producing one more lawn mower at that specific production level.
Understanding the concept of marginal average cost is crucial in economics and business. It provides insights into the additional cost incurred for each additional unit produced, helping businesses make informed decisions about production levels and pricing strategies. In this context,
 specifically tells us about the average cost change at the production quantity of 20 lawn mowers.
specifically tells us about the average cost change at the production quantity of 20 lawn mowers.