Question

A ball of mass 1.86 kilograms is attached to a cord 1.29 meters long and swung in a vertical circle at a constant speed of 5.27 meters per second. What is the centripetal force acting on the ball? Include units in your answer. What is the tension in the cord when the ball is at the bottom of its path? Include units in your answer. What is the tension in the cord when the ball is at the top of its path? Include units in your answer. All answers must be in 3 significant digits.

Answer 1

`\begin{gathered} centripetal\text{ force= 40.044 Newtons} \\ T_(bottom)=58.291\text{ Newtons} \\ T_{\text{top}}=21.79\text{ Newtons} \end{gathered}`

Step-by-step explanation

Step 1

Draw

so

a)centripetal force:

the centripetal force is given by.

`\begin{gathered} F=ma \\ F=m(v^2)/(r) \\ \text{where } \\ F_{C\text{ }}\text{ is the centripetal force} \\ m\text{ is the mass } \\ v\text{ is the velocty } \\ r\text{ is the radius} \end{gathered}`

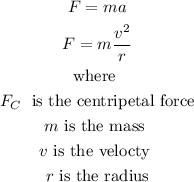
now, replace

`\begin{gathered} F=m(v^2)/(r) \\ F=1.86\text{ kg }\frac{(\text{ 5.27 }(m)/(s))^2}{1.29\text{ m}} \\ F=40.044\text{ Newtons} \end{gathered}`

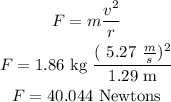
so, the centripetal force is 40.0446 Newtons

b) What is the tension in the cord when the ball is at the bottom of its path?

to find the tension in bottom, we need to add the weigth of the ball,so

`\begin{gathered} \text{weigth}=\text{ mass}\cdot accelofgravity \\ w=mg \end{gathered}`

hence, the tension would be

`\begin{gathered} T_(bottom)=m(v^2)/(r)+mg \\ \end{gathered}`

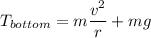
replace

`\begin{gathered} T_(bottom)=m(v^2)/(r)+mg \\ T_(bottom)=40.044\text{ N+(1.86 kg}\cdot9.81\text{ }\frac{\text{m}}{s^2}) \\ T_(bottom)=40.044\text{ N+18.2466 N} \\ T_(bottom)=58.291\text{ N} \end{gathered}`

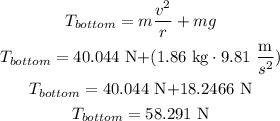
c)What is the tension in the cord when the ball is at the top of its path?

to find the tension in the top we need to subtract the weigth, so

`\begin{gathered} T_{\text{top}}=m(v^2)/(r)-mg \\ replace \\ T_{\text{top}}=40.044\text{ N-18.2466 N} \\ T_{\text{top}}=21.79\text{ Newtons} \end{gathered}`

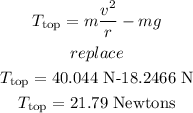
I hope this helps you