Question

Find the minimum value if f(x) = xe^x over [-2,0]

Answer 1

Given function:

`f(x)=xe^x`

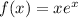
The minimum value of the function can be found by setting the first derivative of the function to zero.

`f^(\prime)(x)=xe^x+e^x`
`\begin{gathered} xe^x+e^x\text{ = 0} \\ e^x(x\text{ + 1) = 0} \end{gathered}`

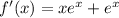
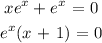
Solving for x:

`\begin{gathered} x\text{ + 1 = 0} \\ x\text{ = -1} \end{gathered}`
`\begin{gathered} e^x\text{ = 0} \\ \text{Does not exist} \end{gathered}`

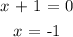
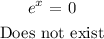
Substituting the value of x into the original function:

`\begin{gathered} f(x=1)=-1* e^{^(-1)}_{} \\ =\text{ -}0.368 \end{gathered}`

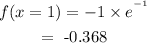
Hence, the minimum value in the given range is (-1, -0.368)