Question

A right triangle has one leg that is 4 more than twice the other. The area of the triangle is 35. Find the length of the sides.

Answer 1

The shorter leg = 5

The longer leg = 14

The hypotenuse = 14.866.....

Explanation:

if we represent the smaller leg as "x" we firstly represent the longer leg as...

Longer leg = 2x + 4

(We can do this based on the question)

Now we need to undersstadn t in a right angle triangle the legs can be used as a height and base. So we can make the following equation.

`A_(triangle) = (bh)/(2)`

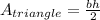
Substitute the lengths of the legs as based and height and get...

`A_(triangle) = ((2x + 4)(x))/(2)`

`35 = (2x^(2) + 4x)/(2)`

`35 = x^(2) + 2x`

`35 = x(x + 2)`

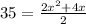
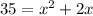
From here we can see that x = 5.

Therefore the lengths are as follows...

The shorter leg = x = 5

The longer leg = 2(5) + 4 = 14

The hypotenuse =
`\sqrt{5^(2) + 14^(2) }`

The hypotenuse =
`\sqrt{5^(2) +14^(2) }`

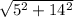
The hypotenuse = 14.866.....

Answer 2

one leg = 5

other leg = 14

Explanation:

let 'x' = length of shorter leg

let '2x + 4' = length of longer leg

A = 1/2bh

35 = 1/2x · 2x + 4

35 = x² + 4

x² + 4 - 35 = 0

(x + 7)(x - 5) = 0

x = -7 and x = 5

We can eliminate -7 as an answer since a length cannot be negative