Question

Question 8, chap 109, sect 5 . part 1 of 110 points A student performs a ballistic pendulum experiment using an apparatus similar to that shown in the figure. Initially the bullet is fired at the block while the block is at rest (at its lowest swing point). After the bullet hits the block, the block rises to its highest position, see dashed block in the figure, and continues swinging back and forth. The following data is obtained: the maximum height the pendulum rises is 6 cm at the maximum height the pendulum subtends an angle of 53.1 ∘, the mass of the bullet is 60 g, and the mass of the pendulum bob is 945 g. The acceleration of gravity is 9.8 m/s 2. Determine the initial speed of the bullet. Answer in units of m/s.

Answer 1

To determine the initial speed of the bullet in the ballistic pendulum experiment, calculate the vertical component of the initial velocity using the maximum height of the pendulum and the equation v =
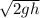`√(2gh)`. The horizontal component of initial velocity is zero. The initial speed of the bullet is the magnitude of initial velocity vector.

Step-by-step explanation:

To determine the initial speed of the bullet in the ballistic pendulum experiment, we need to use the principle of conservation of momentum. When the bullet hits the block, the bullet and the block move together as one system. Considering the pendulum's maximum height and the angle it subtends, we can find the initial velocity of the system using basic trigonometry.

The vertical component of the initial velocity of the block and bullet system can be found using the maximum height of the pendulum. The vertical velocity is given by v =
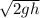`√(2gh)` where g is the acceleration due to gravity and h is the maximum height. Substituting the values of g and h, we can find the vertical component of the initial velocity. The horizontal component of the initial velocity of the system is zero.

Thus, the initial speed of the bullet can be found by calculating the magnitude of the initial velocity vector, which is the square root of the sum of the squares of vertical and horizontal components of velocity.