Question

Hi can I have some help on number 12 please

Answer 1

Given the question in the image, the following are the solution steps to answer the question.

STEP 1: Write the given functions

`\begin{gathered} f(x)=x^2 \\ g(x)=-(x+2)^2-3 \end{gathered}`

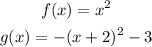
STEP 2: Describe the transformations

Translation to the left/right: Horizontal translation refers to the movement toward the left or right of the graph of a function by the given units. The shape of the function remains the same. It is also known as the movement/shifting of the graph along the x-axis.

To shift, move, or translate horizontally, replace y = f(x) with y = f(x + c) (left by c) or y = f(x - c) (right by c).

Translations up/down: The graph of a function can be moved up, down, left, or right by adding to or subtracting from the output or the input. Adding to the output of a function moves the graph up. Subtracting from the output of a function moves the graph down.

To translate the function up and down, you simply add or subtract numbers from the whole function. If you add a positive number (or subtract a negative number), you translate the function up. If you subtract a positive number (or add a negative number), you translate the function down.

STEP 3: Define the first transformation

STEP 4: Define the vertical transformation

`\begin{gathered} f(x)\Rightarrow f(x)-3 \\ This\text{ shows a vertical transformation downwards by 3 units} \end{gathered}`

STEP 5: Define the final transformation

`\begin{gathered} f(x)\Rightarrow-f(x) \\ This\text{ shows a reflection over the x-axis} \end{gathered}`

Hence, the transformations of f(x) to g(x) are:

Translated 2 units left

Translated 3 units down

Reflected over the x-axis (yes)