Answer:
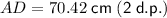
Explanation:
Edge AD of the given triangular-based pyramid is the hypotenuse of right triangle ABD.
To find the length of AD, we first need to determine the length of one of the legs of ΔABD. To do this, we can find the length of BD by applying the tangent trigonometric ratio to right triangle BCD.

In triangle BCD:
- θ = ∠D = 33°
- O = BC = 37 cm
- A = BD
Substitute these values into the tangent ratio and solve for BD:
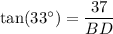
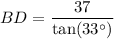
Now, apply the sine trigonometric ratio to right triangle ABD to find the length of AD.

In triangle ABD:
- θ = ∠A = 54°
- O = BD = 37 / tan(33°)
- H = AD
Substitute these values into the sine ratio and solve for AD:
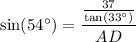
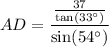
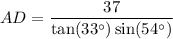
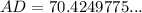
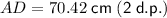
Therefore, the length of edge AD is 70.42 cm, rounded to two decimal places.