Question

Find the length of BC and BE (show work please)

Answer 1

BC = 4 cm

BE = 10.39

Explanation:

ABCD is an isosceles trapezoid.

Measures of base angles of an isosceles trapezoid are equal.

`\therefore m\angle ABC = m\angle DCB`

`\because m\angle DCB = 120\degree`

`\therefore m\angle ABC = 120\degree`

`m\angle ABE = 120\degree-90\degree`

`m\angle ABE = 30\degree`

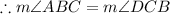
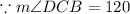
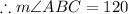
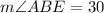
in triangle ABE,

`\cos 30\degree =(BE)/(12)`

`(\sqrt 3)/(2) =(BE)/(12)`

`BE = (\sqrt 3* 12)/(2)`

`BE =6\sqrt 3\: cm`

`BE = 10.39 cm`

`\sin 30\degree =(AE)/(12)`

`(1)/(2) =(AE)/(12)`

`AE = (12)/(2)`

`AE =6 \: cm`

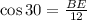
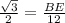
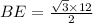
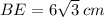
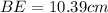
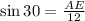
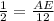
Next, Draw
`CF\perp AD`

FD = AE = 6

EF = 16 - (AE + FD) = 16 - (6+6) = 16-12

EF = 4 cm

BCFE is a rectangle.

Measures of the opposite sides of a rectangle are equal.

Therefore

BC = EF

BC = 4 cm