Question

The acceleration of a particle along a straight line is defined by a=(2t−9)m/s2, where t is in seconds. At t = 0, s = 1 m and v = 10 m/s. 1.) What is the particle's position after t=9 second

Answer 1

Step-by-step explanation:

Knowing that acceleration is the derivative of velocity, and velocity is the derivative of position, we can integrate the acceleration function with respect to t, find the constant, and then repeat the process to find the position function with its respective constant.

`v(t) = \int\(a(t)dt=\int(2t-9)dt = (2t^2)/(2)-9t+C_v`

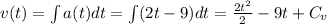
Using t = 0 and v = 10 m/s,

`v(0) = 10 m/s = (0)^2 - 9(0)+C_v`

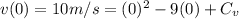
leaving
`C_v` to be 10 m/s.

Then,

`s(t) = \int\(v(t)dt= \int(t^2-9t+10)dt=(t^3)/(3)-(9t^2)/(2)+10t+C_s\\`

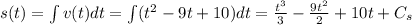
Using t = 0 and s = 1 m

`s(t) = ((0)^3)/(3)-(9(0)^2)/(2)+10(0)+C_s`

leaving
`C_s` to be 1 m.

Plugging in t = 9 seconds into our new equation gives

`((9)^3)/(3)-(9(9)^2)/(2)+10(9)+1`

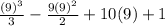
which gives -30.5 m