Question

The admission fee at The Louvre is $5 for children and $16 for adults. Yesterday, 800 people came to The Louvre and $8400 was collected. How many children and how many adults came to The Louvre?​

Answer 1

400 adults and 400 children

Explanation:

adults=a, children=c

1st equation $5c+$16a=$8400

2nd equation a+c=800 people

1st 5c+16a=8400

2nd a+c=800 = a=800-c

substitute 800-c for a in the first equation

5c+16(800-c)=8400

now solve

5c+12800-16c=8400

-11c=-4400

c=400

put 400 in for c in one of the equations

a+400=800

solve

a=400

Answer 2

Children: 400

Adults: 400

Explanation:

Let x be the number of children and y be the number of adults.

We know that the total number of people is 800 and the total amount of money collected is $8400. We can set up the following system of equations to represent this information:

x + y = 800

5x + 16y = 8400

We can solve this system of equations using elimination. Multiplying the top equation by 5, we get:

5x + 5y = 4000

Subtracting this equation to the bottom equation, we get:

Dividing both sides by 11, we get:

`(11y)/(11) =(4400)/(11)`

`\sf y = 400`

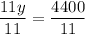
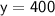
Now that we know the value of y, we can substitute it into the top equation to solve for x.

x + 400 = 800

Subtract 400 on both sides.

x + 400 - 400 = 800 - 400

x = 400

Therefore, there were 400 children and 400 adults at The Louvre yesterday.