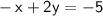Question

Write the equation of the line in point slope form, slope intercept form, and standard form. Through: (1, -2) and (-1,-3)

Answer 1

Equation of the line in:

Point slope form:
`\sf y + 2 =(1)/(2)x - (1)/(2)`

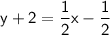
Slope intercept form:
`\sf y =(1)/(2)x - (5)/(2)`

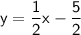
Standard form:
`\sf -x + 2y = -5`

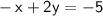
Explanation:

To find the equation of the line passing through the points (1,-2) and (-1,-3), we can use the following steps:

Find the slope of the line.

The slope of the line is calculated as follows:

`\sf Slope = \frac{\textsf{Change in y}}{\textsf{Change in x}}`

`\sf Slope = ( -3-(-2))/(-1-1) \\\\ = ( -1)/(-2) \\\\ = (1)/(2)`

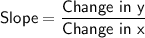
Use the point-slope form to write the equation of the line.

The point-slope form of the equation of the line is as follows:

`\sf y - y_1 = m(x - x_1)`

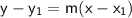
where m is the slope of the line and (x1, y1) is a point on the line.

Using the slope of 1/2 and the point (1, -2), we can write the equation of the line in point-slope form as follows:

`\sf y - (-2) = (1)/(2)(x - 1)`

`\sf y + 2 =(1)/(2)x - (1)/(2)`

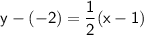
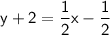
Use the slope-intercept form to write the equation of the line.

The slope-intercept form of the equation of the line is as follows:

y = mx + b

where m is the slope of the line and b is the y-intercept.

To convert the equation of the line from point-slope form to slope-intercept form, we can solve for y:

`\sf y + 2 =(1)/(2)x - (1)/(2)`

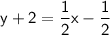
Subtract 2 on both sides:

`\sf y + 2 - 2 =(1)/(2)x - (1)/(2) - 2`

`\sf y =(1)/(2)x + (- 1-2* 2 )/(2)`

`\sf y =(1)/(2)x - (5)/(2)`

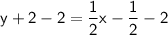
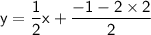
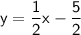
Therefore, the equation of the line in slope-intercept form is :

`\sf y =(1)/(2)x - (5)/(2)`

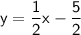
Use the standard form to write the equation of the line.

The standard form of the equation of the line is as follows:

Ax + By = C

where A, B, and C are constants.

To convert the equation of the line from slope-intercept form to standard form, we can multiply both sides of the equation by 2:

`\sf y * 2 =(1)/(2)x * 2 - (5)/(2) * 2`

`\sf 2y = x - 5`

`\sf -x + 2y = -5`

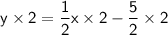
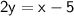
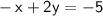
Therefore, the equation of the line in standard form is:

`\sf -x + 2y = -5`