Question

A family of four is spending an average of $793.29 monthly on food but would like to cut back on this expense. If this family is able to decrease their spending by 0.5% every month, what will be their monthly spending on food after one year? Only enter the number, in dollars, rounded to two decimal places.

Answer 1

$746.98

Explanation:

To calculate the family's monthly spending on food after one year with a 0.5% reduction each month, we can use the exponential decay formula:

`\large\boxed{A = P(1 - r)^(t)}`

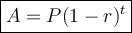
where:

• A is the monthly spending on food after t months.
• P is the initial monthly spend on food.
• r is the monthly reduction rate (in decimal form).
• t is the number of months.

In this case:

• P = $793.29
• r = 0.5% = 0.005
• t = 1 year = 12 months

Substitute these values into the formula and solve for A:

`A = 793.29(1 - 0.005)^(12)`

`A = 793.29(0.995)^(12)`

`A = 793.29(0.9416228069...)`

`A=746.979956497...`

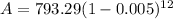
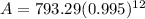
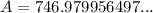
So, the family's monthly spending on food after one year, with a 0.5% reduction each month, will be approximately $746.98 (rounded to the nearest cent).

Answer 2

$746.98

Explanation:

In order t calculate the family's monthly spending on food after one year with a 0.5% decrease every month, we can use the following formula:

Final Monthly Spending = Initial Monthly Spending × (1 - Monthly Decrease Percentage)^(Number of Months)

Where:

• Initial Monthly Spending = $793.29
• Monthly Decrease Percentage = 0.5% (0.005 in decimal form)
• Number of Months = 12 (for one year)

Substitute these values:

`\begin{aligned}\textsf{Final Monthly Spending}& = \$793.29 * (1 - 0.005)^(12) \\\\ &= \$793.29 * (0.995)^(12) \\\\ &= \$793.29 * 0.94162280 \\\\ &= \$746.97995649710 \\\\ &= \$ 746.98 \textsf{( in 2 decimal places)}\end{aligned}`

So, after one year of decreasing their spending by 0.5% every month, the family's monthly spending on food after one year will be approximately $746.98.