Question

1. What is the value of the expression below?

PLEASE GET IT CORRECT AND MAKE THE ANSWER EASY TO UNDERSTAND

Answer 1

`\begin{array}{c}3\cdot\left[\left(30-2^3\right)/ 2+2\:\right]\\\\\boxed{3}\cdot\left[\left(30-\boxed{8}\:\right)/ \boxed{2}+2\:\right]\\\\3\cdot\left[\left(\:\boxed{22}\:\right)/ 2+\boxed{2}\;\right]\\\\3\cdot\left[\:\boxed{11}+2\:\right]\\\\3\cdot\boxed{13}\\\\39\end{array}`

Explanation:

The given expression is:

`3\cdot\left[\left(30-2^3\right)/ 2+2\:\right]`

The PEMDAS rule is an acronym representing the order of operations in math:

• Parentheses
• Exponents
• Multiplication (from left to right)
• Division (from left to right)
• Addition (from left to right)
• Subtraction (from left to right)

Following the order of operations (PEMDAS), we should start with the parentheses inside the square brackets. Inside these, begin by calculating the exponent:

`3\cdot\left[\left(30-8\right)/ 2+2\:\right]`

Now, subtract the numbers inside the parentheses:

`3\cdot\left[\:22/ 2+2\:\right]`

As we still have a set of brackets, we need to perform the calculations inside these brackets before any other operations. Since division should be performed before addition, divide 22 by 2 inside the square brackets:

`3\cdot\left[\:11+2\:\right]`

Now, add the numbers inside the square brackets:

`3\cdot 13`

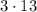
As we have no brackets left, perform the multiplication:

`39`

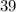
Therefore, the completed calculation is:

`\begin{array}{c}3\cdot\left[\left(30-2^3\right)/ 2+2\:\right]\\\\\boxed{3}\cdot\left[\left(30-\boxed{8}\:\right)/ \boxed{2}+2\:\right]\\\\3\cdot\left[\left(\:\boxed{22}\:\right)/ 2+\boxed{2}\;\right]\\\\3\cdot\left[\:\boxed{11}+2\:\right]\\\\3\cdot\boxed{13}\\\\39\end{array}`

Answer 2

3 [(30-2³)÷2+2]

3 [(30-8)÷2+2]

3 [22÷2+2]

3[11+2]

3[13]

39

Explanation:

To evaluate the expression 3 [(30-2³)÷2+2], we need to follow the order of operations.

The order of operations is as follows:

• Parentheses, brackets, and braces. Any operations inside of parentheses, brackets, or braces should be performed first.
• Exponents. Exponents should be evaluated next.
• Multiplication and division. Multiplication and division should be performed from left to right.
• Addition and subtraction. Addition and subtraction should be performed from left to right.

Therefore, let's solve it using this:

3 [(30-2³)÷2+2]

Solving Parentheses, brackets, and braces.

Solve the bracket.

3 [(30-8)÷2+2]

3 [22÷2+2]

Then, we multiply and divide from left to right:

3[11+2]

Finally, we add and subtract from left to right:

3 [13]

Open the big bracket.

39

Therefore, the value of the expression 3 [(30-2^3)÷2+2] is 39.