Question

Roselle has three cups of popcorn and 6 oz of soda for a total of $246 calories. Carmel has one cup of popcorn and 14 oz of soda for a total of $274 calories. determine the number of calories per cup of popcorn and per ounce of soda

Answer 1

Let 'x' be the number of calories per cup of popcorn, and 'y' be the number of calories per ounce of soda.

Given that 3 cups of popcorn and 6 oz of soda constitute 246 calories,

`3x+6y=246`

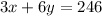
Also given that 1 cups of popcorn and 14 oz of soda constitute 274 calories,

`x+14y=274`

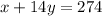
Solve the equations using Elimination Method.

Subtract 3 times equation 2 from equation 1,

`\begin{gathered} (3x+6y)-3(x+14y)=246-3(274) \\ 3x+6y-3x-42y=246-822 \\ -36y=-576 \\ y=16 \end{gathered}`

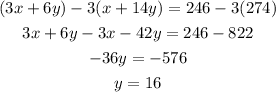
Substitute this value in equation 1, to obtain 'x' as,

`\begin{gathered} 3x+6(16)=246 \\ 3x+96=246 \\ 3x=150 \\ x=50 \end{gathered}`

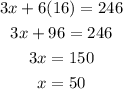
Thus, the solution of the system of equations is x=50 and y=16.

Therefore, there are 50 calories per cup of popcorn, and 16 calorie per ounce of soda.