Problem 17
The graph is shown below.
The domain is
 which is found by solving
which is found by solving
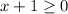 . This is done to ensure that the stuff under the square root is not negative. Note the left-most point of the graph has x = -1 as its x coordinate.
. This is done to ensure that the stuff under the square root is not negative. Note the left-most point of the graph has x = -1 as its x coordinate.
The domain in interval notation is
 we have a square bracket at -1 and a curved parenthesis at infinity.
we have a square bracket at -1 and a curved parenthesis at infinity.
The range is
 based on what the graph shows. This is directly tied to the +3 at the end of the function. The parent's function max value is y = 0, so that plus 3 shifts everything up 3 units so that the new translated function has a max of y = 3.
based on what the graph shows. This is directly tied to the +3 at the end of the function. The parent's function max value is y = 0, so that plus 3 shifts everything up 3 units so that the new translated function has a max of y = 3.
The range in interval notation is
![(-\infty, 3]](https://img.qammunity.org/2022/formulas/mathematics/college/v5idolzs0egvqb9c9nu1zj21ruzrok2ogs.png) we use a square bracket to include 3 as part of the interval.
we use a square bracket to include 3 as part of the interval.
Throughout the entire function, the curve is going downhill as we move from left to right. The graph shows this. We could also use a table of values to see that as x gets bigger, y gets smaller.
So the function is never increasing. The function decreases on the interval (-1, infinity) which is the entire domain.
=====================================================
Problem 18
The graph is shown below. It's in a separate attachment.
The domain and range are the set of all real numbers. The graph shows that the curve extends forever to the left and right. Also, the graph extends forever upward and downward (regardless if that growth seems really slow).
The domain and range in interval notation is
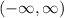 to indicate the entire real number line.
to indicate the entire real number line.
The graph goes uphill as we read from right to left, so the function is increasing on the interval
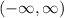 . In other words, no matter where you are, you're going uphill if you move from left to right. This rules out the function ever decreasing.
. In other words, no matter where you are, you're going uphill if you move from left to right. This rules out the function ever decreasing.
We can use a table of values to see that the function is increasing if we cannot rely on the graph. As x gets bigger, so does y.