Question

Write the equation of the line in slope intercept form that goes through the points (0,6) and (1,5)

Answer 1

`y=-x+6`

Explanation:

Given: Points (0,6) and (1,5).

Assuming you want the equation in slope intercept form, here's the following step-by-step explanation.

Slope Intercept Form:
`y=mx+b`

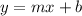
1.) Find the slope (m) using the formula:

`(y_(2) -y_(1) )/(x_(2) -x_(1) )`

`m = (5-6)/(1-0) = (-1)/(1) = -1`

`m=-1`

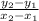
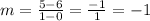
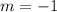
2.) Find the y-intercept (b)

We need to isolate
`b` in
`y=mx+b`

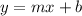
To do this, we need to substitute all variables, but
`b`.

To substitute y, We can use either
`y_(2)` or
`y_(1)`.

To substitute x, We can use either
`x_(2)`
`x_(1)`.

To substitute m, We can use the slope in this case, which we found out was 1

For example, we can use the point (0,6)

`6=(-1)(0)+b`

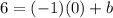
This gives us

`6=0+b\\`

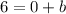
Which finally gives us

`6=b`

We can use the symmetry property of equality (which states if a=b, then b=a) to flip the equation.

That gives us,
`b=6`

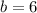
Our final answer is,
`y= -x+6`

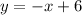
Disclaimer: While we strive to provide accurate information online, it's essential to verify answers with your teacher when they pertain to your coursework. Online sources may contain errors, and individual classroom requirements can vary. We encourage you to use the information here as a reference but recommend confirming its accuracy and appropriateness with your instructor, as they play a vital role in guiding your learning. Your teacher is there to support you, and reaching out to them with questions or concerns is a valuable part of your educational journey.