Answer:
A. { -5,2}
Explanation:
In order t find the solution set of the equation x² + 3x - 4 = 6 , we need to first move all terms to one side of the equation and then solve for x.
Here's the equation:
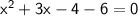
Now, simplify the equation:
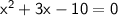
To solve this quadratic equation, we can use the quadratic formula:
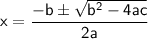
where
- a is the coefficient of a², which is 1,
- b is the coefficient of x, which is 3
- c is the constant term, which is -10.
Now
Substitute these values into the quadratic formula and solve for x.
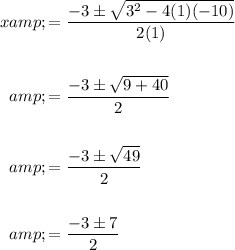
Now, we have two possible solutions:
When positive
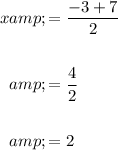
When negative
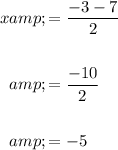
Therefore, the solution set of the equation is A. { -5,2}.