Question

What is the value of x to the nearest tenth on problem 5

Answer 1

Step-by-step explanation:

In problem 5, we can see that there is a right triangle with legs x and 16 and a hypotenuse equal to (x + 8).

So, by Pythagorean theorem, we can write the following equation

`(x+8)^2=x^2+16^2`

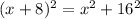
Now, we can expand the left side

`\begin{gathered} x^2+2(8)(x)+8^2=x^2+16^2 \\ x^2+16x+64=x^2+256 \end{gathered}`

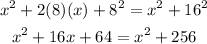
Then, subtract x² from both sides

`\begin{gathered} x^2+16x+64-x^2=x^2+256-x^2 \\ 16x+64=256 \end{gathered}`

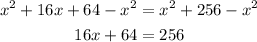
Subtract 64 from both sides

`\begin{gathered} 16x+64-64=256-64 \\ 16x=192 \end{gathered}`

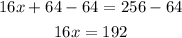
Finally, divide by 16

`\begin{gathered} (16x)/(16)=(192)/(16) \\ \\ x=12 \end{gathered}`

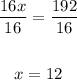
Therefore, the value of x is 12