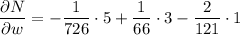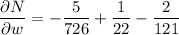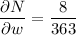Question

Help please. Use the chain rule

Answer 1

`(\partial N)/(\partial u)=(9)/(242)`

`(\partial N)/(\partial v)=-(1)/(22)`

`(\partial N)/(\partial w)=(8)/(363)`

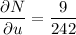
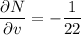
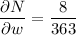
Explanation:

Partial derivatives are the rates at which a multivariable function changes with respect to specific individual variables, while keeping all other variables constant.

To find the partial derivatives δN/δu, δN/δv and δN/δw when u = 3, v = 5, w = 8, first calculate the partial derivatives of p, q and r with respect to u, v and w:

`(\partial p)/(\partial u)=(\partial)/(\partial u)u+(\partial)/(\partial u)vw=1+0=1`

`(\partial q)/(\partial u)=(\partial)/(\partial u)v+(\partial)/(\partial u)uw=0+w=w`

`(\partial r)/(\partial u)=(\partial)/(\partial u) w+(\partial)/(\partial u) uv=0+v=v`

`(\partial p)/(\partial v)=(\partial)/(\partial v)u+(\partial)/(\partial v)vw=0+w=w`

`(\partial q)/(\partial v)=(\partial)/(\partial v)v+(\partial)/(\partial v)uw=1+0=1`

`(\partial r)/(\partial v)=(\partial)/(\partial v)w+(\partial)/(\partial v) uv=0+u=u`

`(\partial p)/(\partial w)=(\partial)/(\partial w)u+(\partial)/(\partial w)vw=0+v=v`

`(\partial q)/(\partial w)=(\partial)/(\partial w)v+(\partial)/(\partial w)uw=0+u=u`

`(\partial r)/(\partial w)=(\partial)/(\partial w)w+(\partial)/(\partial w) uv=1+0=1`

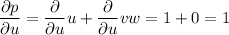
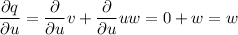
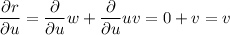
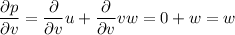
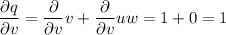
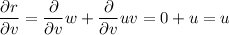
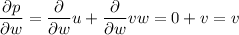
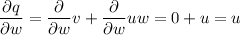
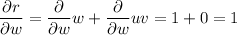
Now, calculate the partial derivatives of N with respect to p, q and r by applying the quotient rule:

`\begin{aligned}(\partial N)/(\partial p)&=((\partial)/(\partial p)(p+q)(p+r)-(\partial)/(\partial p)(p+r)(p+q))/((p+r)^2)\\\\&=(1 \cdot (p+r)-1\cdot(p+q))/((p+r)^2)\\\\&=(p+r-p-q)/((p+r)^2)\\\\&=(r-q)/((p+r)^2)\end{aligned}`

`\begin{aligned}(\partial N)/(\partial q)&=((\partial)/(\partial q)(p+q)(p+r)-(\partial)/(\partial q)(p+r)(p+q))/((p+r)^2)\\\\&=(1\cdot (p+r)-0\cdot(p+q))/((p+r)^2)\\\\&=(p+r)/((p+r)^2)\\\\&=(1)/(p+r)\end{aligned}`

`\begin{aligned}(\partial N)/(\partial r)&=((\partial)/(\partial r)(p+q)(p+r)-(\partial)/(\partial r)(p+r)(p+q))/((p+r)^2)\\\\&=(0\cdot (p+r)-1\cdot(p+q))/((p+r)^2)\\\\&=-(p+q)/((p+r)^2)\end{aligned}`

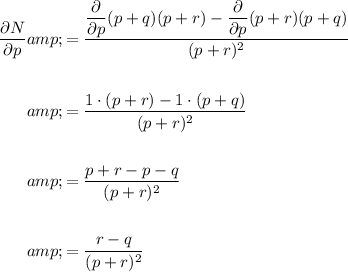
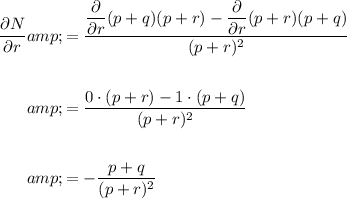
Find the values of p, q and r by substituting u = 3, v = 5 and w = 8 into their equations:

`p=u+vw=3+5\cdot8=43`

`q=v+uw=5+3\cdot8=29`

`r=w+uv=8+3\cdot5=23`

Evaluate δN/δu, δN/δv and δN/δw when p = 43, q = 29 and r = 23:

`(\partial N)/(\partial p)=(23-29)/((43+23)^2)=-(1)/(726)`

`(\partial N)/(\partial q)=(1)/(43+23)=(1)/(66)`

`(\partial N)/(\partial r)=-(43+29)/((43+23)^2)=-(2)/(121)`

`\hrulefill`

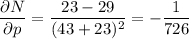
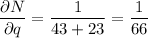
Apply the multivariable chain rule to find δN/δu:

`(\partial N)/(\partial u)=(\partial N)/(\partial p)\cdot (\partial p)/(\partial u)+(\partial N)/(\partial q)\cdot(\partial q)/(\partial u)+(\partial N)/(\partial r)\cdot(\partial r)/(\partial u)`

`(\partial N)/(\partial u)=(r-q)/((p+r)^2)\cdot1+(1)/(p+r)\cdot w-(p+q)/((p+r)^2)\cdot v`

`(\partial N)/(\partial u)=-(1)/(726)\cdot1+(1)/(66)\cdot8-(2)/(121)\cdot5`

`(\partial N)/(\partial u)=-(1)/(726)+(4)/(33)-(10)/(121)`

`(\partial N)/(\partial u)=(9)/(242)`

`\hrulefill`

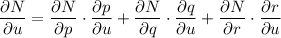
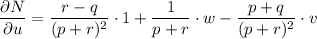
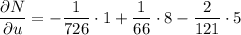
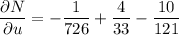
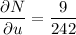
Apply the multivariable chain rule to find δN/δv:

`(\partial N)/(\partial v)=(\partial N)/(\partial p)\cdot (\partial p)/(\partial v)+(\partial N)/(\partial q)\cdot(\partial q)/(\partial v)+(\partial N)/(\partial r)\cdot(\partial r)/(\partial v)`

`(\partial N)/(\partial v)=(r-q)/((p+r)^2)\cdot w+(1)/(p+r)\cdot1-(p+q)/((p+r)^2)\cdot u`

`(\partial N)/(\partial v)=-(1)/(726)\cdot8+(1)/(66)\cdot1-(2)/(121)\cdot3`

`(\partial N)/(\partial v)=-(4)/(363)+(1)/(66)-(6)/(121)`

`(\partial N)/(\partial v)=-(1)/(22)`

`\hrulefill`

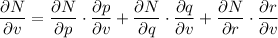
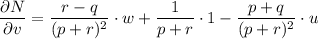
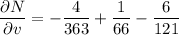
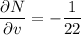
Apply the multivariable chain rule to find δN/δw:

`(\partial N)/(\partial w)=(\partial N)/(\partial p)\cdot(\partial p)/(\partial w)+(\partial N)/(\partial q)\cdot(\partial q)/(\partial w)+(\partial N)/(\partial r)\cdot(\partial r)/(\partial w)`

`(\partial N)/(\partial w)=(r-q)/((p+r)^2)\cdot v+(1)/(p+r)\cdot u-(p+q)/((p+r)^2)\cdot1`

`(\partial N)/(\partial w)=-(1)/(726)\cdot5+(1)/(66)\cdot3-(2)/(121)\cdot1`

`(\partial N)/(\partial w)=-(5)/(726)+(1)/(22)-(2)/(121)`

`(\partial N)/(\partial w)=(8)/(363)`