Question

A snack bar started the day with 128 bags of

popcorn. At the end of the first hour, half of
the bags had been sold. Half of the remaining
bags were sold during the second hour: Based
on this pattern, how many hours did it take
before the snack bar had only 1 bag of
popcorn lefto

Answer 1

7 hours

Explanation:

From the given information, we can determine that the snack supply has a half-life of 1 hour. This means that the decay in supply (rather, the rate of people buying snacks) is relative to the current supply.

In other words, every hour, the supply decreases by 1/2 of its original amount at the start of the hour.

We can represent this with the half-life equation:

`N(t) = N_0 \cdot \left((1)/(2)\right)^(\!t/h)`

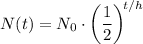
where N(t) is the current amount of something (at time t), N₀ is the initial amount (the amount when time t = 0), and h is the supply's half life.

We are given the following values:

• 
  `N_0 = 128\text{ snacks}`
• 
  `h = 1 \text{ hr}`

We are solving for time t when
`N(t) = 1`:

↓ plugging in the known values

`1 = 128 \cdot \left((1)/(2)\right)^(\! t/1)`

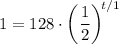
↓ simplifying the exponent ...
`t/1 = t`

`1 = 128 \cdot \left((1)/(2)\right)^(\! t)`

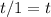
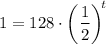
↓ dividing both sides by 128

`(1)/(128) = \left((1)/(2)\right)^(\! t)`

↓ taking the
`\log_(\,1/2)` of both sides

`\log_(\, 1/2)\left[(1)/(128)\right] = t`

↓ simplifying the left side ...
`\log_(\,1/a)\!\left((1)/(b)\right) = \log_a(b)`

`\log_(2)(128) = t`

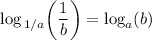
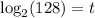
↓ evaluating the left side

`\boxed{7 = t}`

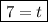
So, it took 7 hours for the snack bar to only have 1 bag of snacks left.