Question

Use the chain rule to find

dw
dt
W =
dw
dt
xey/z, x=t7, y = 4-t, z = 7+ 3t

number 2

Answer 1

`\frac{\text{d}w}{\text{d}t} = e^{(4-t)/(7+3t)}\left[(63t^8+275t^7+343t^6)/((7+3t)^2)\right]`

Explanation:

Given equations:

`w=xe^{(y)/(z)}`

`x=t^7`

`y=4-t`

`z=7+3t`

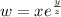
To find dw/dt for the given functions w, x, y, and z, use the chain rule. The chain rule states that if you have a composite function like w(x(t), y(t), z(t)), then the derivative of w with respect to t is given by:

`\frac{\text{d}w}{\text{d}t} = (\partial w)/(\partial x) \cdot \frac{\text{d}x}{\text{d}t} + (\partial w)/(\partial y) \cdot \frac{\text{d}y}{\text{d}t} + (\partial w)/(\partial z) \cdot \frac{\text{d}z}{\text{d}t}`

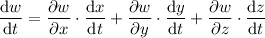
Partial derivatives are the rates at which a multivariable function changes with respect to specific individual variables, while keeping all other variables constant.

Find the partial derivatives of w with respect to x, y, and z, using the chain rule where necessary.

To find δw/δx, treat y and z as constants:

`\begin{aligned}(\partial w)/(\partial x) &=e^{(y)/(z)} \cdot (\partial )/(\partial x)(x)\\\\(\partial w)/(\partial x)&=e^{(y)/(z)}\end{aligned}`

To find δw/δy, treat y and z as constants:

`(\partial w)/(\partial y) =x \cdot (\partial )/(\partial y)\left(e^{(y)/(z)}\right)`

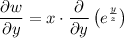
Apply the chain rule:

`(\partial w)/(\partial y) =x \cdot e^{(y)/(z)}\cdot (\partial)/(\partial y)\left((y)/(z)\right)`

`(\partial w)/(\partial y) =x \cdot e^{(y)/(z)}\cdot (1)/(z)`

`(\partial w)/(\partial y) =\frac{e^{(y)/(z)}x}{z}`

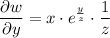
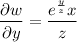
To find δw/δz, treat x and y as constants:

`(\partial w)/(\partial z) =x \cdot (\partial )/(\partial z)\left(e^{(y)/(z)}\right)`

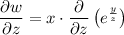
Apply the chain rule:

`(\partial w)/(\partial z) =x \cdot e^{(y)/(z)}\cdot (\partial)/(\partial z)\left((y)/(z)\right)`

`(\partial w)/(\partial z) =x \cdot e^{(y)/(z)}\cdot \left(-(y)/(z^2)\right)`

`(\partial w)/(\partial z) =-\frac{e^{(y)/(z)}xy}{z^2}`

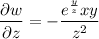
Next, calculate the derivatives of x, y, and z with respect to t:

`\frac{\text{d}x}{\text{d}t}=7t^6`

`\frac{\text{d}y}{\text{d}t}=-1`

`\frac{\text{d}z}{\text{d}t}=3`

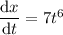
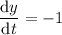
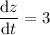
Now, substitute these derivatives and the partial derivatives into the chain rule formula:

`\frac{\text{d}w}{\text{d}t} = (\partial w)/(\partial x) \cdot \frac{\text{d}x}{\text{d}t} + (\partial w)/(\partial y) \cdot \frac{\text{d}y}{\text{d}t} + (\partial w)/(\partial z) \cdot \frac{\text{d}z}{\text{d}t}`

`\frac{\text{d}w}{\text{d}t} = e^{(y)/(z)} \cdot 7t^6 + \frac{e^{(y)/(z)}x}{z} \cdot (-1) + \left(-\frac{e^{(y)/(z)}xy}{z^2}\right)\cdot 3`

`\frac{\text{d}w}{\text{d}t} = 7t^6e^{(y)/(z)} - \frac{e^{(y)/(z)}x}{z} -\frac{3e^{(y)/(z)}xy}{z^2}`

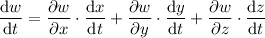
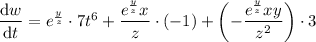
`\frac{\text{d}w}{\text{d}t} = e^{(y)/(z)}\left[7t^6 - (x)/(z) -(3xy)/(z^2)\right]`

Plug in the expressions for x, y and z:

`\frac{\text{d}w}{\text{d}t} = e^{(4-t)/(7+3t)}\left[7t^6 - (t^7)/(7+3t) -(3t^7(4-t))/((7+3t)^2)\right]`

`\frac{\text{d}w}{\text{d}t} = e^{(4-t)/(7+3t)}\left[(7t^6(7+3t)^2)/((7+3t)^2) - (t^7(7+3t))/((7+3t)^2) -(3t^7(4-t))/((7+3t)^2)\right]`

`\frac{\text{d}w}{\text{d}t} = e^{(4-t)/(7+3t)}\left[(7t^6(7+3t)^2-t^7(7+3t)-3t^7(4-t))/((7+3t)^2)\right]`

`\frac{\text{d}w}{\text{d}t} = e^{(4-t)/(7+3t)}\left[(63t^8+275t^7+343t^6)/((7+3t)^2)\right]`

Therefore, dw/dt is:

`\large\boxed{\boxed{\frac{\text{d}w}{\text{d}t} = e^{(4-t)/(7+3t)}\left[(63t^8+275t^7+343t^6)/((7+3t)^2)\right]}}`

Please note that you may need to give the derivative as an expanded form (or some other form).