Question

HELP NEEDED!

Write down an algebraic expression for each of the following statements.

A. Subtract the cube root of the product of x and 3y from the square of the sum of a and b.

B. The total value of x 20-cent coins and y 5-dollar notes in cents.

Answer 1

A)
`(a+b)^(2)- \sqrt[3]{x . 3y}`

B) 20 x + 500 y

Explanation:

A. Subtract the cube root of the product of x and 3y from the square of the sum of a and b.

A = The square of the sum of a and b is
`(a+b)^(2)`

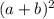
B = The cube root of the product of x and 3y is
`\sqrt[3]{x . 3y}`

They want us to subtract B from A so B - A, therefore the following.

`(a+b)^(2)- \sqrt[3]{x . 3y}`

B. The total value of x 20-cent coins and y 5-dollar notes in cents.

20x cents is already provided as they want the expression in cents. Moving on to the $5 dollar note. We will have to convert this $5 into cents in order to fulfill the question requirements.

Convert:

1 dollar = 100 cents

5 dollars = 100x5 = 500 cents

Therefore, 5y dollars = 500y cents. Finally, we end up with the following answer.

20 x cents + 500 y cents

20 x + 500 y