Answer:
m∠AOC = 85°
Explanation:
Since Line segment OC splits m∠AOB into two angles
So, we can use the following equation:
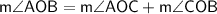
We are given that m∠AOB = 155° and m ∠COB is 15° less than AOC.
This means that we can write m ∠COB as m∠AOB - 15°. Substituting these values into the equation above, we get:
155° = m∠AOC + (m∠AOC - 15°)
Combining like terms, we get:
155° = 2AOC - 15°
Adding 15° to both sides of the equation, we get:
155° + 15° = 2AOC - 15° + 15°
170° = 2 m∠AOC
Dividing both sides of the equation by 2, we get:
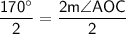
m∠AOC = 85°
Therefore, m∠AOC = 85°