Final answer:
To find the number of photons produced in a laser pulse, you can use the equation E = nhf, where E is the energy of one photon, n is the number of photons, h is the Planck constant, and f is the frequency of the light. By calculating the energy of one photon using the equation E = hc/λ and then dividing the total energy of the laser pulse by the energy of one photon, we find it to be 4.27 x
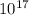
Step-by-step explanation:
To calculate the number of photons produced in a laser pulse, we need to use the equation E = nhf, where E is the energy of one photon, n is the number of photons, h is the Planck constant, and f is the frequency of the light.
First, we need to calculate the energy of one photon using the formula E = hc/λ, where λ is the wavelength of the light. Plugging in the values, we get:
E = (6.63 x
 J s)(3.00 x
J s)(3.00 x
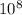 m/s) / (453 x
m/s) / (453 x
 m) = 4.37 x
m) = 4.37 x
 J
J
Next, to find the number of photons, we divide the total energy of the laser pulse by the energy of one photon:
n = (0.187 J) / (4.37 x
 J) = 4.27 x
J) = 4.27 x
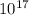 photons
photons