Question

Determine an equation for the pictured graph. Write your answer in factored form.

Answer 1

`f(x)=-x(x+1)^2(x-2)`

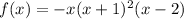
Explanation:

The root of a polynomial is a point on the graph where the curve intersects or crosses the x-axis, meaning that the function equals zero at that point.

From observation of the given graph, the roots of the polynomial are:

• x = -1
• x = 0
• x = 2

According to the Factor Theorem, if a polynomial f(x) has a root at x = a, then (x - a) is a factor of f(x).

The multiplicity of a root refers to the number of times the associated factor appears in the factored form of the equation of a polynomial.

When a root has a multiplicity of one, the graph of the polynomial function crosses the x-axis at that particular value of x. The concavity of the graph remains the same as it approaches and passes through the x-axis. Therefore, from observation of the given graph, the roots with multiplicity one are x = 0 and x = 2. This means the factors for these roots are (x - 0) and (x - 2).

When a root has a multiplicity of two, the graph of the polynomial function touches or "bounces off" the x-axis at that particular value of x without crossing it. Hence, the root with multiplicity two is x = -1. This means the factor for this root is (x + 1)².

So, a possible factored form of the graphed function is:

`f(x)=a(x-0)(x-2)(x+1)^2`

`f(x)=ax(x-2)(x+1)^2`

`f(x)=ax(x+1)^2(x-2)`

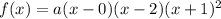
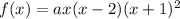
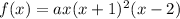
From observation of the graph, the curve appears to pass through point (1, 4). Therefore, to find the leading coefficient (a), we can substitute point (1, 4) into the function and solve for a:

`\begin{aligned}f(1)=a(1)(1+1)^2(1-2)&=4\\a(2)^2(-1)&=4\\-4a&=4\\a&=-1\end{aligned}`

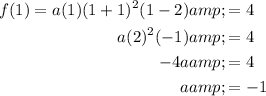
So, the equation of the graphed function in factored form is:

`f(x)=-x(x+1)^2(x-2)`

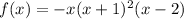
This equation satisfies the observed characteristics of the graph.