Question

Can someone Plss help me i don’t know how to do this… it’s a Precalc question

Answer 1

Answer:
`2\text{x}^4-14\text{x}^2+12`

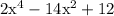
This is the same as writing 2x^4 - 14x^2 + 12 when typing it out on a keyboard.

=====================================================

Step-by-step explanation

The three given roots are:
`-1, 1, √(6)`

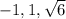
Because all of the polynomial's coefficients are integers, it must mean that the last missing root is
`-√(6)`.

This is because the radical roots come in conjugate pairs of the form
`a+b√(c) \ \text{ and } a-b√(c)` when the polynomial has integer coefficients.

The two roots x = -1 and x = 1 lead to the quadratic
`(\text{x}-1)(\text{x}+1) = \text{x}^2-1 = 0`

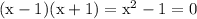
Note we have a difference of squares.

The two roots
`-√(6) \ \text{ and } \ √(6)` lead to
`(\text{x}-√(6))(\text{x}+√(6)) = \text{x}^2 - (√(6))^2 = \text{x}^2-6`

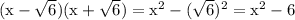
This is also a difference of squares.

---------------------

Let's multiply those results

`(\text{x}^2-1)(\text{x}^2-6)\\\\=\text{x}^2(\text{x}^2-6)-1(\text{x}^2-6)\\\\=\text{x}^4-6\text{x}^2-\text{x}^2+6\\\\=\text{x}^4-7\text{x}^2+6\\\\`

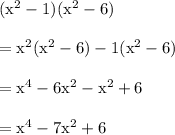
Therefore,

`(\text{x}^2-1)(\text{x}^2-6)=\text{x}^4-7\text{x}^2+6\\\\`

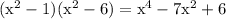
That quartic polynomial has the four roots:
`-1, \ 1, \ -√(6), \ \text{ and } √(6)`

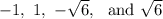
The last step is to double every term so that the 6 at the end turns into 12 (since your teacher requires the constant term be 12).

We arrive at the final answer
`2\text{x}^4-14\text{x}^2+12`

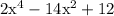
A tool like WolframAlpha or GeoGebra's CAS feature can be used to verify that we have the correct answer.