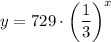Question

Write an equation that models the values in the table: Responses y=13x+243 y is equal to 1 third x plus 243 y=729(13)x y is equal to 729 times 1 third to the x th power y=13(3)x y is equal to 1 third times 3 to the x th power y=3x y is equal to 3 x

Answer 1

• y is equal to 729 times 1/3rd to the xth power

Task :

• To work out the function that models the values in the given table.

Solution :

To find out which among the given options is the equation that models the values given, we'll plug in the value of x as 1 and check if the resultant value of y = 243.

#1

• 
  `y=13x+243`
• 
  `y = 13 * 1 + 243 \\ y = 246≠243`

Thus, No.

#2

• 
  `y = (1)/(3)x + 243`
• 
  `y = (1)/(3) * 1 + 243 \\ y = (1 + 729)/(3) = (730)/(3) \\ y = 243.33 \: ≠243`

Thus, No.

#3

• 
  `y=729(13)x`
• 
  `y = 729(13) * 1 \\ y = 729 * 13 \\ y = 9477≠ \: 243`

Thus,No.

#4

• 
  `y = 729 * ((1)/(3) ) {}^(x) \\`
• 
  `y = 729 * ( (1)/(3) ) {}^(1) \\ y = 729 * (1)/(3) \\ y = 243 = 243`

Thus, Yes,this is the equation that models the table.

#5

• 
  `y=13(3)x`
• 
  `y = 13(3) * 1 \\ y = 39 ≠243`

Thus,No.

#6

• 
  `y = (1)/(3) * 3 {}^(x) \\`
• 
  `y = (1)/(3) * 3 {}^(1) \\ y = (1)/(3) * 3 \\ y = 1≠243`

Thus,No.

#7

• 
  `y = 3x`
• 
  `y = 3 * 1 \\ y = 3≠243`

Thus,No.

Therefore, Option (4) y is equal to 729 times one-third to the xth power is the correct answer.

Answer 2

`\textsf{B)} \quad y=729\cdot \left((1)/(3)\right)^x`

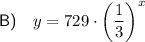
Explanation:

The data in the given table models an exponential function, since each y-value is one-third of the preceding y-value.

The general formula of an exponential function is:

`\boxed{\begin{minipage}{9 cm}\underline{General form of an Exponential Function}\\\\$y=ab^x$\\\\where:\\\phantom{ww}$\bullet$ $a$ is the initial value ($y$-intercept). \\ \phantom{ww}$\bullet$ $b$ is the base (growth/decay factor) in decimal form.\\\end{minipage}}`

As the y-values decrease by the constant factor 1/3, the base of the function is b = 1/3:

`y=a\cdot \left((1)/(3)\right)^x`

To find the value of a, we can substitute one of the (x, y) points from the table into the equation and solve for a. Using point (1, 243):

`243=a\cdot \left((1)/(3)\right)^1`

`243=(1)/(3)a`

`243\cdot 3=(1)/(3)a \cdot 3`

`a=729`

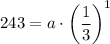
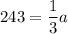
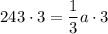
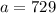
Therefore, the equation that models the values in the given table is:

`y=729\cdot \left((1)/(3)\right)^x`