Question

Assuming Earth to be a sphere of radius 4000​ miles, how many miles north of the Equator is City​ A, if it is 39° north from the​ Equator?

Answer 1

`\bold{ANSWER:}`
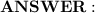
2,154.32 miles north


`\bold{EXPLANATION:}`

To determine the distance north of the Equator for City A, we can use the concept of latitude. The Earth's equator is at 0° latitude, and as we move north, the latitude increases.

Given that City A is located 39° north from the Equator, we can calculate the distance north of the Equator by multiplying the angular distance by the circumference of the Earth.

Circumference of the Earth = 2 * π * radius

Plugging in the values:

Circumference of the Earth = 2 * π * 4000 miles

Now, to find the distance north of the Equator for City A:

Distance north of the Equator= (39° / 360°) *

Circumference of the Earth
Calculating this:

Distance north of the Equator = (39/360) * (2 * π 4000 miles)

Therefore, City A is approximately 2,154.32 miles north of the Equator.