Question

Find the length of the legs.(4,4)[](-2,-2)[?]Enter the number thatbelongs in the green boxEnter

Answer 1

We have a right triangle and we have to find the length of the legs.

We first analyse the hypotenuse.

It is a line that is defined by two points: (4,4) and (-2,-2).

The line passes through the center of coordinates, but we will check it:

The slope can be calculated as:

`m=(y_2-y_1)/(x_2-x_1)=(4-(-2))/(4-(-2))=1`

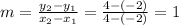
We can now write the slope-point equation as:

`\begin{gathered} y-y_0=m(x-x_0) \\ y-4=1(x-4) \\ y-4=x-4 \\ y=x \end{gathered}`

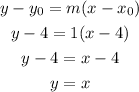
Then, we know that the equation of the line that defines the hypotenuse is y=x.

If the legs are parallel to the axis, we can find the angle that is defined by the hypotenuse and the horizontal leg as:

`\begin{gathered} \tan (\theta)=m=1 \\ \theta=\arctan (1)=45\degree \end{gathered}`

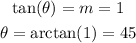
As we have an angle of 45 degree for one leg, the other has to have an equal angle, as 180-90-45=45 (Note: we are substracting from the sum of the 3 angles, 180 degrees, the already known angles, 90 and 45 degrees, so we are left with 45 degrees that correspond to the third angle).

If the two angles for the legs are equal, their lengths are equal too.

So we can start by calculating the length of the hypotenuse: it is the distance between (4,4) and (-2,-2).

`\begin{gathered} D=\sqrt[]{(x_2-x_1)^2+(y_2-y_1)^2}=\sqrt[]{(4-(-2))^2+(4-(-2))^2} \\ D=\sqrt[]{6^2+6^2}=\sqrt[]{2\cdot6^2}=6\sqrt[]{2} \end{gathered}`

Then, we can write the Pythagorean theorem as (a and b are the legs, and c is the hypotenuse):

`\begin{gathered} a^2+b^2=c^2 \\ a=b\longrightarrow2a^2=c^2=(6\sqrt[]{2})^2=36\cdot2=72 \\ a^2=(72)/(2) \\ a^2=36 \\ a=\sqrt[]{36} \\ a=b=6 \end{gathered}`

Answer: the length of the legs is 6 units.