For |2x-7|>1:
This absolute value inequality results in two inequalities: 2x-7>1 or 2x-7<-1.
Solve these inequalities to find the answer:
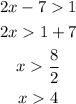
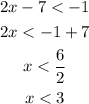
It means that the answer is x>4; x<3.
For |2x-7|<1:
This results in one complex inequality: -1<2x-7<1.
Solve it to find the answer:
![\begin{gathered} -1<2x-7<1 \\ -1+7<2x<1+7 \\ 6<2x<8 \\ (6)/(2)<strong>It means that the answer is 3For |2x-7|=1:From the equation we can conclude that 2x-7=1 or 2x-7=-1.Solve these equations to find the answer:[tex]\begin{gathered} 2x-7=1 \\ 2x=1+7 \\ x=(8)/(2) \\ x=4 \end{gathered}]()
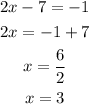 The answer is x=3; x=4.
The answer is x=3; x=4.