Question

Question is shown in image below. Answer format is also shown in image.

Answer 1

For |2x-7|>1:

This absolute value inequality results in two inequalities: 2x-7>1 or 2x-7<-1.

Solve these inequalities to find the answer:

`\begin{gathered} 2x-7>1 \\ 2x>1+7 \\ x>(8)/(2) \\ x>4 \end{gathered}`
`\begin{gathered} 2x-7<-1 \\ 2x<-1+7 \\ x<(6)/(2) \\ x<3 \end{gathered}`

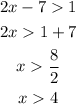
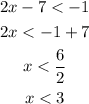
It means that the answer is x>4; x<3.

For |2x-7|<1:

This results in one complex inequality: -1<2x-7<1.

Solve it to find the answer:

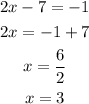`\begin{gathered} 2x-7=-1 \\ 2x=-1+7 \\ x=(6)/(2) \\ x=3 \end{gathered}`The answer is x=3; x=4.