Question

6. What would be the angle of elevation to the top of a radio transmitting tower that is 100 m tall and 400 m from the observer? Answer to the nearest degree.

7. A) Find the unknown length, x, to one decimal
place.
B) Find the unknown angle, a, to the nearest degree.

Answer 1

Answer:

Problem 6:

The angle of elevation to the top of a radio transmitting tower that is 100 m tall and 400 m from the observer is approximately 14 degrees.

Problem 7:

A) The unknown length `x` in Problem 7 is approximately 55.9 m.

B) The unknown angle `a` in Problem 7 is approximately 42 degrees.

Explanation:

Problem 6:

The angle of elevation can be found using the tangent of the angle, which is the ratio of the opposite side (height of the tower) to the adjacent side (distance from the observer).

So, we have:

`$$\tan(\theta) = (opposite)/(adjacent) = (100m)/(400m) = 0.25$$`

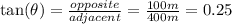
To find the angle, we take the inverse tangent (or arctan) of 0.25. Using a calculator, we find that:

`$$\theta = \arctan(0.25) \approx 14^\circ$$`

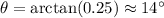
Problem 7:

A) The unknown length `x` can be found using the Pythagorean theorem in a right triangle, which states that the square of the hypotenuse is equal to the sum of the squares of the other two sides. So, we have:

`$$x = √(75^2 - 50^2) \approx 55.9m$$\\`

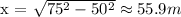
B) The unknown angle `a` can be found using the sine of the angle, which is the ratio of the opposite side (the side of length 50m) to the hypotenuse (the side of length 75m).

So, we have:

`$$\sin(a) = (opposite)/(hypotenuse) = (50m)/(75m) = (2)/(3)$$`

To find the angle, we take the inverse sine (or arcsin) of 2/3. Using a calculator, we find that:

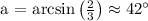
`$$a = \arcsin\left((2)/(3)\right) \approx 42^\circ$$`

:)