Question

A.

13.1 m
105⁰
Work out the perimeter of triangle ABC.
Give your answer to 3 significant figures.
B
48⁰
C

Answer 1

29.4 m

Explanation:

sine formula (ASA) : length with the opposite angle facing it


`(sin(105 degree))/(13.1)=(sin(48 degree))/(x)`
x= 10.1 which is side AB
The sum of angles for a triangle should equal = 180 , so angle A =27 degree
use the equation again to find BC

`(sin(105 degree))/(13.1)=(sin(27 degree))/(x)`

x= 6.2 , side BC

perimeter = AB+BC+AC , sum of all sides
perimeter = 13.1 + 10.1 + 6.2
perimeter =29.4 m

Answer 2

Answer:

29.336 m

Explanation:

To find the perimeter of the triangle.

Given:

In ∆ ABC

• m ∠B = 48°
• m ∠C = 105°
• m ∠A =180° - 105° - 48° = 27°
• AC = 13.1 m

Solution:

To find the perimeter of the triangle, we can use the following formula:

Perimeter = a + b + c

where a, b, and c are the lengths of the sides of the triangle.

We are given the length of side AC (b) is 13.1 m. We also know the measures of angles B and C. To find the lengths of the other two sides, we can use the law of sines:

`\sf (a )/(sin(A) )= (b )/( sin(B) )= (c )/( sin(C))`

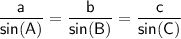
We can rewrite this formula as follows:

`\sf c = b \cdot ( sin(B) )/(sin(C))`

`\sf a = b \cdot ( sin(A) )/(sin(C))`

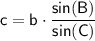
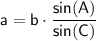
We know that the length of side AC is 13.1 m, and the measures of angles B and C are 48° and 105°, respectively. We can use the above formulas to find the lengths of the other two sides:

`\sf BC(a) = 13.1 \cdot ( sin(27^\circ) )/(sin(105^\circ)) \\\\ \approx 6.157 m`

`\sf AB( c) = 13.1 \cdot ( sin(48^\circ) )/(sin(105^\circ ))\\\\ \approx 10.079m`

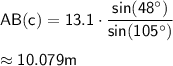
Now that we know the lengths of all three sides of the triangle, we can find the perimeter:

Perimeter = AB + BC + AC

= 10.079 m + 6.157 m + 13.1 m

= 29.336 m

Therefore, the perimeter of the triangle is 29.336 m